Python 作為當今普及的編程語言,其中一個優勢在於能夠快速驗證一些在統計學裡預測的結果。
概論:什麼是統計學的預測?
比方說,我們想要知道在拋 2 次硬幣的時候,有什麼可能的結果(outcome)以及每個結果的概率(probability)。
常理來說,如果拋 1 次硬幣出現公(Head)和字(Tail)的概率是一樣的話,以下的情況應各佔 1/4 的概率:
- 2 次公(Head+Head)
- 1 次公和 1 次字(Head+Tail)
- 1 次字和 1 次公(Tail+Head)
- 2 次字(Tail+Tail)
如果我們在現實生活想驗證這個預測,其中一個可能的實驗是:
- 把一個硬幣重複拋 100 次
- 紀錄每一次拋硬幣的結果(例如 1:公, 2:字, 3:字, 4:公….)
- 把拋硬幣的紀錄以每 2 個結果組合,分成 50 等份(例如 1-2: 公字,3-4:字公…)
- 計算「公公」、「公字」、「字公」、「字字」出現的頻率(frequency),例如以下的表:
| 結果(outcome) | 頻率(frequency) | 樣本概率(Sampled odds) |
|---|---|---|
| 公公 | 10 | 10/50 = 20% |
| 公字 | 15 | 15/50 = 30% |
| 字公 | 9 | 9/50 = 18% |
| 字字 | 16 | 16/50 = 32% |
當然,在現實生活裡進行這個實驗並不是非常有效:
- 如果我們想要比較準確的結果,我們需要進行非常多次的實驗,例如把硬幣拋 10,000 次
- 實驗會受環境因素影響,例如拿來拋的硬幣重量分佈(centre of mass)並不完美
而電腦/編程可以讓我們極速地進行多次的實驗,所以對於我們驗證統計學的預測非常有用!
以下我們使用同一個實驗來看看如何使用電腦進行預測吧!
概論:電腦裡的統計實驗與偽代碼(pseudo-code)
電腦其中一個重要的功能,是它很懂得生成隨機值(sampling from distributions)。
就如我們可以拋硬幣生成隨機的結果一樣,電腦亦有機制生成隨機的結果,而且它可以非常快速地生成極多的隨機值。
因此,我們可以使用電腦簡化我們的統計實驗,而不需要不斷地拋硬幣去驗證結果。
如果我們以一段簡單的 Python 偽代碼表示:
# 先定義一個字典(dictionary)儲存結果
result = {
"公公": 0,
"公字": 0,
"字公": 0,
"字字": 0,
}
# 進行 100,000 次實驗
for i in range(1, 10 ** 5):
# 生成兩個 0 至 1 中間的隨機值,如果隨機值大於 0.5 定義為「公」,否則是「字」
first_coin_result = "公" if generate_random_number() > 0.5 else "字"
second_coin_result = "公" if generate_random_number() > 0.5 else "字"
# 把對應的結果 +1
result[first_coin_result + second_coin_result] +=1
# 印出實驗的的結果
for k, v in result.items():
print(k + " 的出現概率是 " + v / (10 **5))
如果我們把這個歸納(generalize)成任何的統計學實驗,那麼 Python 的偽代碼可以是:
# 先定義一個字典(dictionary)儲存結果
result = {
"outcome_1": 0,
"outcome_2": 0,
...
}
# 進行 100,000 次實驗
for i in range(1, 10 ** 5):
# 生成 0 至 1 中間的隨機值
random_number = generate_random_number()
# 使用某些方法定義結果
outcome = some_function(random_number)
# 把對應的結果 +1
result[outcome] +=1
# 印出實驗的的結果
for k, v in result.items():
print(k + " 的出現概率是 " + v / (10 **5))
實戰 1:用 Python 驗證拋硬幣的預期概率
有以上的基礎,我們可以學習如何用 Python 去驗證我們一開始預期的概率吧!
我們會在這篇教學使用免費、免安裝的 Google Colab Notebook。如果您不知道如何使用 Google Colab,可以參考這篇教學:新手 1/3:5 分鐘免安裝學習 Python?Google Colab Notebook 幫緊您!
Python 內建的 random.choice
在我們進行實驗前,我們先要回到剛才其中一個我們沒有提及的問題:如何在 Python 生成隨機值?
上一個段落裡我們只用了 generate_random_number() 作為一個籠統的說法。具體來說,我們有許多不同的 Python library 可以生成隨機值。這裡我們先解釋比較常用的一個:random。
顧名思義,random 就是與隨機值息息相關的 library。其中,我常用的功能是這個 random.choice 的功能。
這個功能讓您可以透過提供一個列表(或 iterable 的東西),隨機選出列表其中一個值。舉例說,假如我們想要生成擲骰子的結果,可以使用一下的方法:
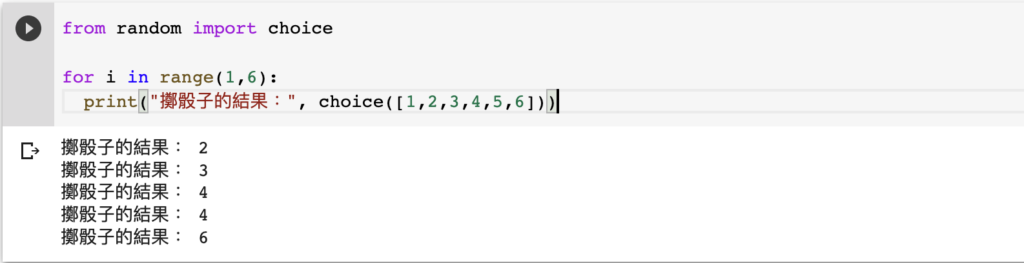
from random import choice
for i in range(1,6):
print("擲骰子的結果:", choice([1,2,3,4,5,6]))
註:先按一下綠色按鈕 “Run” 執行代碼,讓您能在 IPython Shell 看到編程結果!
正如上面所見,random.choice([1,2,3,4,5,6]) 會生成 1-6 其中一個整數。
假如我們紀錄下足夠多次的結果,會發現 1-6 出現的概率是差不多的(無限接近 1/6)。這是因為 random.choice() 的設計是會以一樣的概率生成每一個子項(item)。
使用上面的邏輯完成任務!
有了 random.choice() 的加持以後,我們可以使用剛剛偽代碼同樣的邏輯去研究拋硬幣的結果了!
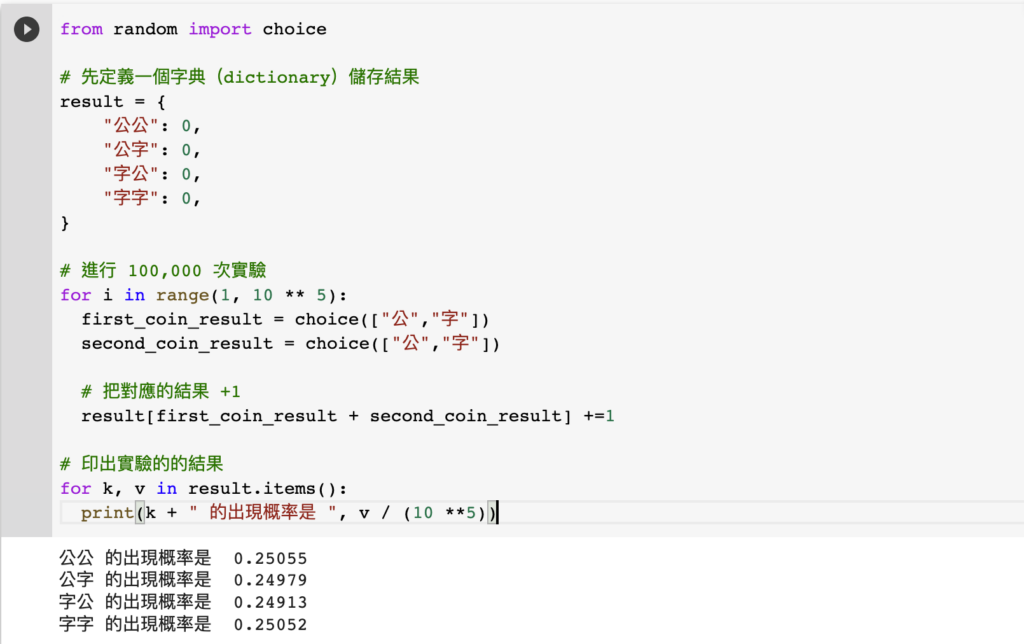
from random import choice
# 先定義一個字典(dictionary)儲存結果
result = {
"公公": 0,
"公字": 0,
"字公": 0,
"字字": 0,
}
# 進行 100,000 次實驗
for i in range(1, 10 ** 5):
first_coin_result = choice(["公","字"])
second_coin_result = choice(["公","字"])
# 把對應的結果 +1
result[first_coin_result + second_coin_result] +=1
# 印出實驗的的結果
for k, v in result.items():
print(k + " 的出現概率是 ", v / (10 **5))
註:先按一下綠色按鈕 “Run” 執行代碼,讓您能在 IPython Shell 看到編程結果!
經過 Python 的計算以後,我們得出了約莫 25% (1/4)的機會得到「公公」、「公字」、「字公」、「字字」的結果。這比人手計算划算的多了!
實戰 2:加入圖表研究趨勢
另一個有趣的小實驗是我們可以研究一下不同個案的概率是否在實驗裡大概一致。
比方說,我們想要知道,如果我們進行 100、1,000、100,000 個拋硬幣實驗,我們會否得出每個結果大概出現 25、250、25,000 次。
我們先來看看略為改動了一下的代碼:
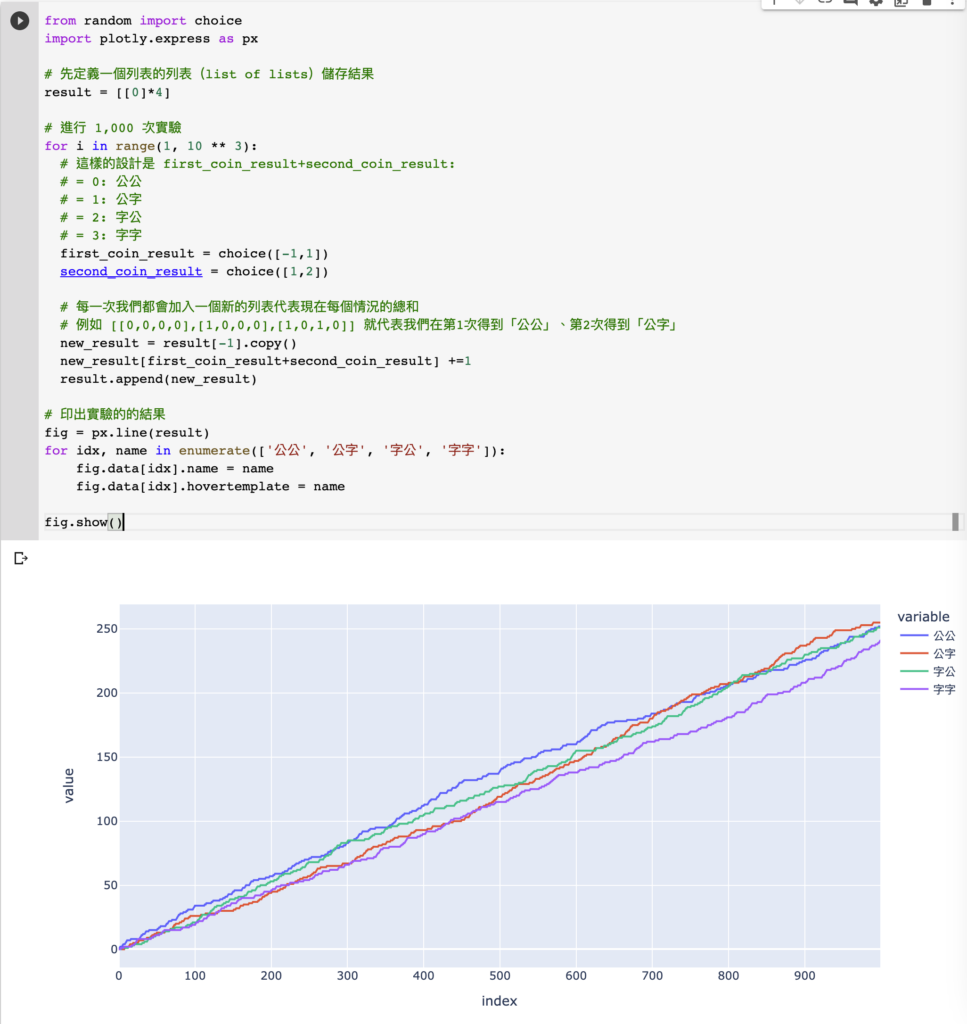
from random import choice
import plotly.express as px
# 先定義一個列表的列表(list of lists)儲存結果
result = [[0]*4]
# 進行 1,000 次實驗
for i in range(1, 10 ** 3):
# 這樣的設計是 first_coin_result+second_coin_result:
# = 0: 公公
# = 1: 公字
# = 2: 字公
# = 3: 字字
first_coin_result = choice([-1,1])
second_coin_result = choice([1,2])
# 每一次我們都會加入一個新的列表代表現在每個情況的總和
# 例如 [[0,0,0,0],[1,0,0,0],[1,0,1,0]] 就代表我們在第1次得到「公公」、第2次得到「公字」
new_result = result[-1].copy()
new_result[first_coin_result+second_coin_result] +=1
result.append(new_result)
# 印出實驗的的結果
fig = px.line(result)
for idx, name in enumerate(['公公', '公字', '字公', '字字']):
fig.data[idx].name = name
fig.data[idx].hovertemplate = name
fig.show()
這裡我們有幾個重點:
- 我們想把
result的儲存方式改變一下,讓我們可以研究每一次拋硬幣後,每一個結果的分佈。比方說,我們頭 3 次拋到「公公」、「公字」、「公公」的話,我們的result是[[0,0,0,0],[1,0,0,0],[1,1,0,0],[2,1,0,0]] - 我們最後會生成一張圖表,裡面的 4 條線代表每一次拋硬幣後,每一個結果共出現了多少次。
當然,我們會預期圖表裡面:
- 每條線最終值是大約 250
- 每一點 X 軸對應每條線的值應該是 X 軸值的 1/4。舉例說,當 X 軸是 400 的時候,我們預計每條線的值約是 100
從上述的圖表裡,我們看到,如果我們使用 1,000 個實驗,那麼這個結果還是比 250 偏離了少許(例如「字字」約 240,其他都大於 250)。我們是否有方法改善這個結果?
做更多的實驗會使結果更準確
這裡我們必須提及一個統計學的道理:如果我們進行更多的實驗,那麼得出的結果應該會更趨近我們的預期(即大數定律 Law of Large Numbers)。
我們先以一張圖表開始:
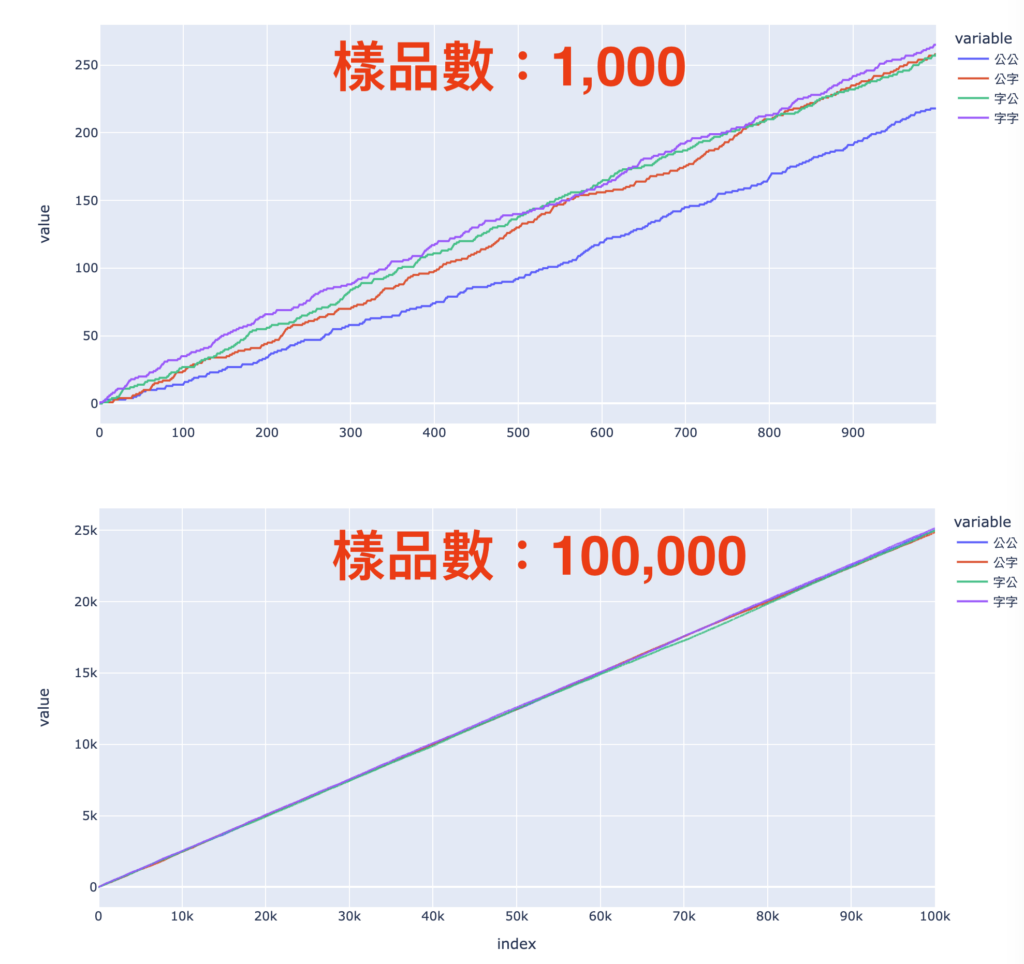
留意我們這 2 張圖都是從上一個段落的代碼生成,只不過我們在上圖進行了 1,000 個實驗,在下圖進行了 100,000 個實驗。
上圖的偏差看起來頗大的,特別是「公公」的數量只有約 210。下圖的偏差看起來非常少,這些結果看似非常接近 1/4。
因此,我們如果想使用電腦模擬統計實驗,其中一個重要的元素是使我們的樣品數(sampling size)增加,讓我們得出的結果更趨向預期。
教學完整代碼
最後送給大家這篇教學的 Google Colab 完整代碼。如果您不懂得使用免安裝又好用的 Google Colab Notebook,記得閱讀這篇教學了:新手 1/3:5 分鐘免安裝學習 Python?Google Colab Notebook 幫緊您!
結語
希望您喜歡這篇關於統計學實驗與 Python 的文章吧!接下來我們會發掘更多有趣的概率/統計問題,讓我們透過 Python 解答難題吧!























